szybko
hermenegilda: Oblicz pole czworokąta o podanych wierzchołkach: A(1,5), B(2,4), C(4,51), D(3,81).
8 cze 21:26
sushi_ gg6397228:
to juz bylo wczoraj lub dwa dni temu, poszukaj sobie
8 cze 21:28
hermenegilda: a nie możesz pomóc
8 cze 21:30
Saizou : 92,5
8 cze 21:32
hermenegilda: nie ma takiej odpowiedzi i mi też taki wynik wyszedł wcześniej jak liczyłam ale to jest źle
8 cze 21:32
Saizou : taka musi być odpowiedź bo tak podaje geogebra
8 cze 21:36
hermenegilda: ok rozumiem ja tez liczylam i tak mi wychodziło ale odpowiedzi są takie
98,23
68
109
121,5
120
115
8 cze 21:39
8 cze 21:41
hermenegilda: i ja mam taki sam błąd
8 cze 21:42
8 cze 21:42
123:
 http://www.zadania.info/d284/1893405
http://www.zadania.info/d284/1893405
Policz sobie ze wzoru podanego na tej stronce (jest on ww tablicach maturalnych dostępnych na
maturze). Poprowadź przekątną i będziesz miał/a 2 trójkąty o 1 wspólnym boku (rys.).
P
czworokąta = P
ΔABD + P
ΔBCD
8 cze 21:45
Mila: Może są inne dane. Sprawdź druk.
Wynik 92,5.
8 cze 22:23
hermenegilda: A(1,5), B(2,4), C(4,51), D(3,81).
takie same
8 cze 22:48
Mila: Skąd Ty bierzesz te zadania?
8 cze 23:24
Gustlik:
 123
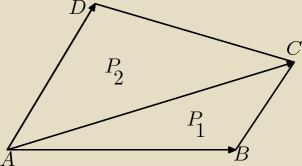
123 pomysł masz dobry, tylko lepiej to liczyć bezpośrednio z wyznacznika wektorów niż tym
ciężko strawnym i długim jak trasa z Warszawy do Pekinu wzorem na pole trójkąta. Zresztą ten
wzór wywodzi się właśnie z wyznacznika wektorów.
A(1,5), B(2,4), C(4,51), D(3,81)
AB
→=[2−1, 4−5]=[1, −1]
AC
→=[4−1, 51−5]=[3, 46]
AD
→=[3−1, 81−5]=[2, 76]
Liczę pola trójkatów P
1 i P
2 z wyznacznika wektorów:
Wyznacznik wektorów:
d(AB
→, AC
→)=
| 1 −1 |
| 3 46 |
=1*46−(−1)*3=46+3=49
| | 1 | | 49 | |
P1= |
| |d(AB→, AC→)|= |
| =24,5 |
| | 2 | | 2 | |
d(AC
→, AD
→)=
| 3 46 |
| 2 76 |
=3*76−46*2=228−92=136
| | 1 | | 136 | |
P2= |
| |d(AC→, AD→)|= |
| =68 |
| | 2 | | 2 | |
Odp: P
cał=24,5+68=92,5
Wektorową metodę obliczania pól wyjaśniłem tutaj:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .
O wiele łatwiej. Po co sobie komplikować życie tasiemcowymi wzorami, w których można się 20
razy pomylić?
Pozdrawiam

9 cze 10:15
hermenegilda: W zamkowych podziemiach znajdują się 18 skrzyń otwieranych różnymi kluczami. Masz pęk
składający się z 100 kluczy, wśród których znajdują się 18 właściwych. Ile co najwyżej prób
należy wykonać, aby mieć pewność że dobraliśmy właściwe klucze do skrzyń?
9 cze 10:48
 http://www.zadania.info/d284/1893405
Policz sobie ze wzoru podanego na tej stronce (jest on ww tablicach maturalnych dostępnych na
maturze). Poprowadź przekątną i będziesz miał/a 2 trójkąty o 1 wspólnym boku (rys.).
Pczworokąta = PΔABD + PΔBCD
http://www.zadania.info/d284/1893405
Policz sobie ze wzoru podanego na tej stronce (jest on ww tablicach maturalnych dostępnych na
maturze). Poprowadź przekątną i będziesz miał/a 2 trójkąty o 1 wspólnym boku (rys.).
Pczworokąta = PΔABD + PΔBCD
 123 pomysł masz dobry, tylko lepiej to liczyć bezpośrednio z wyznacznika wektorów niż tym
ciężko strawnym i długim jak trasa z Warszawy do Pekinu wzorem na pole trójkąta. Zresztą ten
wzór wywodzi się właśnie z wyznacznika wektorów.
A(1,5), B(2,4), C(4,51), D(3,81)
AB→=[2−1, 4−5]=[1, −1]
AC→=[4−1, 51−5]=[3, 46]
AD→=[3−1, 81−5]=[2, 76]
Liczę pola trójkatów P1 i P2 z wyznacznika wektorów:
Wyznacznik wektorów:
d(AB→, AC→)=
| 1 −1 |
| 3 46 |
=1*46−(−1)*3=46+3=49
123 pomysł masz dobry, tylko lepiej to liczyć bezpośrednio z wyznacznika wektorów niż tym
ciężko strawnym i długim jak trasa z Warszawy do Pekinu wzorem na pole trójkąta. Zresztą ten
wzór wywodzi się właśnie z wyznacznika wektorów.
A(1,5), B(2,4), C(4,51), D(3,81)
AB→=[2−1, 4−5]=[1, −1]
AC→=[4−1, 51−5]=[3, 46]
AD→=[3−1, 81−5]=[2, 76]
Liczę pola trójkatów P1 i P2 z wyznacznika wektorów:
Wyznacznik wektorów:
d(AB→, AC→)=
| 1 −1 |
| 3 46 |
=1*46−(−1)*3=46+3=49
